6.2 Introduksjon til maskinlæring med kNN
6.2.2 Kontrollspørsmål
- For hvilke typer responsvariabler bruker vi KNN?
- Hvordan fungerer KNN teoretisk sett?
- Hva er den praktiske tolkningen av KNN?
- Hvordan påvirker valget av \(k\) måten KNN fungerer på?
- Hvordan velger vi \(k\)?
6.2.3 Teori
Kanskje har du allerede hørt om maskinlæring, “data science”, prediktiv modellering, “business analytics”, etc., og kanskje har du fått med deg at disse tingene virkelig er i vinden for tiden. Som akademisk institusjon skal vi selvsagt være på vakt mot å la popularitet være en avgjørende faktor for hva vi driver med, men, som en kollega så treffende uttrykte seg: “Internett er kommet for å bli.” Det skjer utrolig mye verdiskapning når vi får tak i den verdifulle informasjonen som ligger gjemt i de store datamengdene, og næringslivet skriker etter kompetanse. NHH har som svar på dette opprettet masterprofilen “Business Analytics (BAN)” (som ironisk nok er blitt superpopulær!), og det er naturlig å gi en liten smakebit på hva det går ut på i MET4. Det herlige er at vi ikke trenger å dykke så dypt i detaljene for å få brukbar innsikt i hva som skjer.
Overgangen fra logistisk regresjon er naturlig. Vi bruker det vi kan fra regresjonsanalyse til å sette opp en modell der vi forklarer utfallet i en dummyvariabel ved hjelp av et sett forklaringsvariable i allerede observerte data. I første omgang kan vi si at den moderne anvendelsen av logistisk regresjon (kall det gjerne en form for maskinlæring) er å bruke data til å estimere sammenhengen mellom \(X\)-ene og responsvariabelen \(Y\), og så bruke denne sammengengen til å predikere \(Y\) for nye \(X\).
Artikkelen To explain or to predict av Galit Shmueli forklarer distinksjonen mellom det å forklare og det å predikere godt, og skal være noenlunde lesbar for en interessert student.
Eksempelet fra logistisk regresjon er et godt eksempel på en anvendelse: Vi predikerer sannsynligheten for at kunder vil misligholde gjelden i fremtiden, basert på karakteristika vi kan observere nå. Slike sannsynligheter kan vi mate inn i en strategisk analyse for å bestemme oss hvem som skal få innvilget nye lån, men på en systematisk måte der vi sørger for at vi oppnår nødvendige profittmarginer og håndterer risiko på en fornuftig måte, og kan ta hensyn til f.eks. etiske avveininger. Selv om vi ut fra eget behov for profitt og innenfor en akseptabel risikoprofil kan tilby nye lån til kunder med 15% sannsynlighet for å havne i betalingsproblemer, bør vi likevel gjøre det? Poenget her er at du ikke kan gjøre slike vurderinger før du faktisk kan estimere sannsynligheten for mislighold! Statistikken er bunnplanken, og blir mer og mer relevant etter hvert som vi innser at svarene ligger i å analysere data.
Vi går videre til et annet eksempel. En teleoperatør med abonnementskunder ser at det er en systematikk i hvilke kunder som sier opp avtalene sine. Ved å se på spredningsplottet under (rød prikk = kunde som har sagt opp abonnementet), ser det ut til at nye kunder med dyre abonnementer har en tendens til å forlate oss. Kan vi sette opp en klassifiseringsregel der som vi kan anvende på alle kundene våre, som automatisk plukker ut kunder som har f.eks. mer enn 50% sannsynlighet for å si opp? Denne listen kan vi så sende videre til markedsavdelingen, som kan sette i verk forebyggende tiltak (f.eks. lokke de inn i bindende avtaler…?), og vi kan oppnå en umiddelbar gevinst.
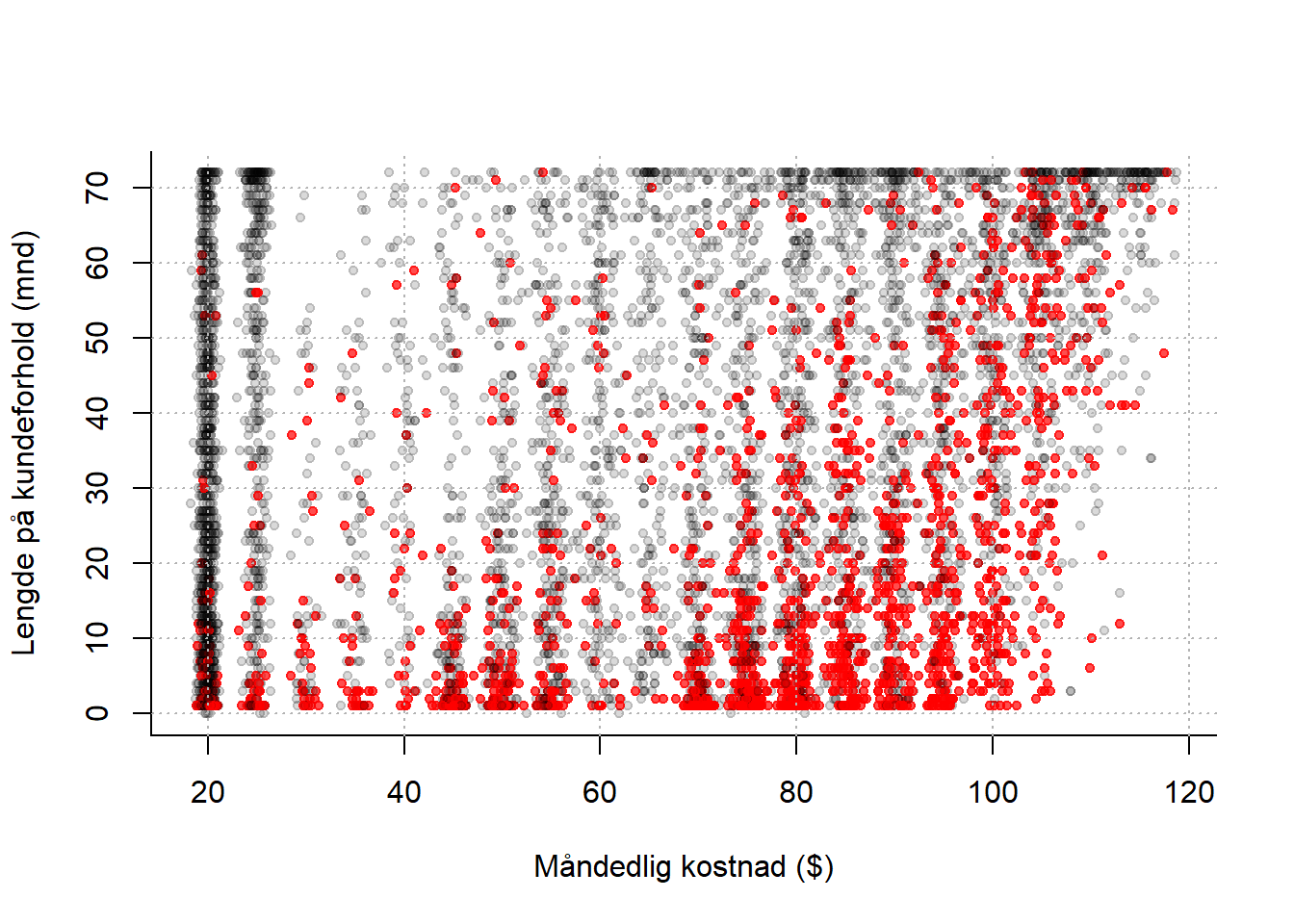
Figur 6.1: Røde prikker er kunder som har sagt opp abbonnementet sitt, svarte prikker er kunder som ikke har gjort det. Finn den optimale avveiningen mellom systematikk og tilfeldig variasjon.
Vi kan angripe dette datasettet på to måter:
- Vi estimerer sannsynligheter ved hjelp av logistisk regresjon. Den stramme strukturen gjør at klassifiseringsgrensen alltid utgjør en rett linje i koordinatsystemet.
- Vi ser også på en annen klassifiseringsregel: kNN (k nearest neighbours), som ikke bruker sannsynlighetsmodeller eller regresjonsparametre til å klassifisere, men heller er en enkel regel basert på følgende prinsipp:
Hvis et flertall av kundene som er mest lik meg har sagt opp, er det mer enn 50% sannsynlig at også jeg vil si opp.
Her bruker vi litt tid på detaljer, men det handler i grunn bare om å lage en presis definisjom om hvem vi definerer som de kundene som ligner mest på meg, og svaret er de \(k\) kundene som ligger nærmest meg i koordinatsystemet.
På samme måte som for logistisk regresjon kan vi lese mer om kNN i ISLR. På s. 39–42 står det hvordan teknikken fungerer, og i forelesningsnotatene og det medfølgende scriptet ser vi hvordan det kan gjøres i praksis.
Når vi forstår hvordan kNN fungerer, er neste steg å reflektere litt over hvordan vi har tenkt å velge parameteren \(k\) i praksis. Vi så i forelesningen at:
Vi kan ikke velge \(k\) for liten. Da ser vi for mye på støy og tilfeldigheter. Vi kan enkelt tenke oss at jeg er en lavrisikokunde, selv om de to kundene som er nærmest meg i koordinatsystemet sa opp av en eller annen grunn. Hvis vi velger \(k = 3\), vil jeg likevel bli klassifisert som høyrisiko og bli bombardert med unødvendig reklame (som i seg selv kan gjøre stor skade!) Hadde vi heller valgt \(k = 50\) eller \(k=500\) ville disse to raringene ikke bli tatt hensyn til, men blitt dominert av alle andre i området som faktisk ikke har sagt opp. Altså: vi kan ikke henge oss for mye opp i detaljene og den tilfeldige variasjonen!
Vi kan heller ikke velge \(k\) for stor, for det vil til slutt nærme seg en situasjon det det bare blir en avstemning mellom alle kundene i datasettet. Det er flest kunder som ikke sier opp avtalen, så da blir alle kunder klassifisert som lavrisiko. Altså: vi vil heller ikke ignorere variasjonen i datamaterialet! Hele poenget er jo å lære noe nyttig fra hvordan prikkene fordeler seg i koordinatsystemet.
I Figur 6.1 kan du prøve følgende: En liten \(k\) svarer til å se nøye på figuren (putt hodet ditt helt inntil skjermen!), og virkelig legge merke til hvor hver eneste en av de røde prikkene befinner seg. Å velge en større \(k\) svarer til å trekke lenger bort, og kanskje begynne å myse litt, slik at du får øye på systematikken, nemlig at det røde dominerer nede til høyre i figuren. Til slutt står du i rommet ved siden av med lukkede øyne, og da ser du plutselig ingenting! Et eller annet sted i mellom der ønsker vi å være.
Kryssvalidering er en systematisk og generell måte å velge k for KNN (og tilsvarende parametre i andre maskinlæringsmetoder), som litt lenger enn å bare dele datasettet inn i trenings- og testdata ISLR behandler temaet på s. 181–186, men det er forholdsvis teknisk og skrevet i lys av noen metoder som vi ikke har sett på i MET4.