8.3 Seminar 3 - Regresjon I
- Se på den estimerte regresjonskurven under:
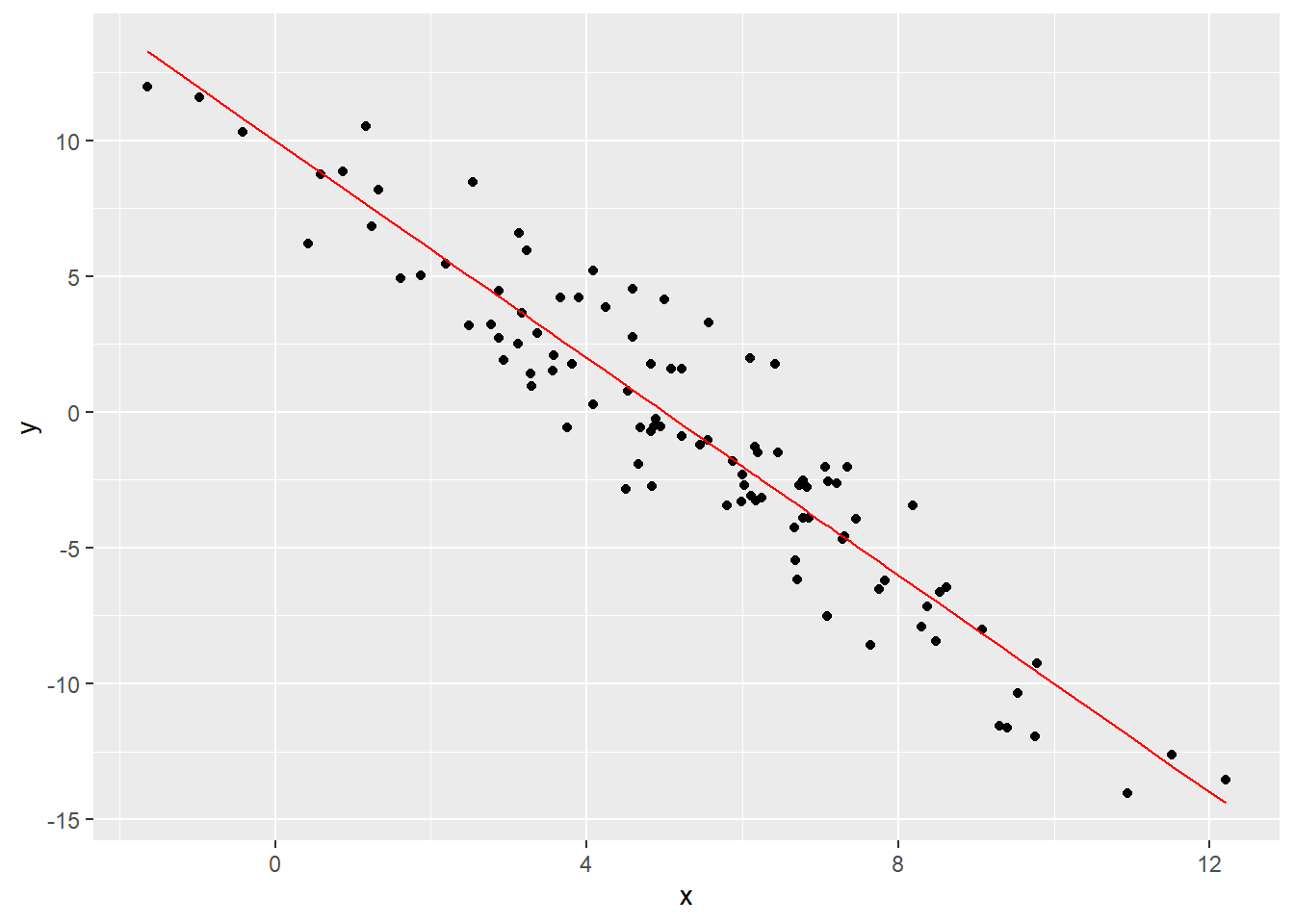
- Bestem hvilke av de følgende parameterestimatene som kan være riktig:
- \(\hat{\beta}_0 = 5\), \(\hat{\beta}_1 = -3\)
- \(\hat{\beta}_0 = 10\), \(\hat{\beta}_1 = 4\)
- \(\hat{\beta}_0 = -4\), \(\hat{\beta}_1 = 2\)
- \(\hat{\beta}_0 = 10\), \(\hat{\beta}_1 = -2\)
- Bestem hvilke av de følgende utsagn om den estimerte korrelasjonen mellom \(X\) og \(Y\) og andel forklart variasjon (\(R^2\)) som er riktig:
- Korrelasjonen er \(-0.94\) andel forklart variasjon er \(-0.88\).
- Korrelasjonen er \(0.94\) andel forklart variasjon er \(0.88\).
- Korrelasjonen er \(-0.94\) andel forklart variasjon er \(0.88\).
- Korrelasjonen er \(1\) andel forklart variasjon er \(0.88\).
- Under ser du et residualplott og et QQ-plot for en regresjonsanalyse. Hvilke brudd på antagelsene for lineær regresjon ser du? Dersom alle andre kriterier er oppfylt, hvilke konsekvenser har disse bruddene?
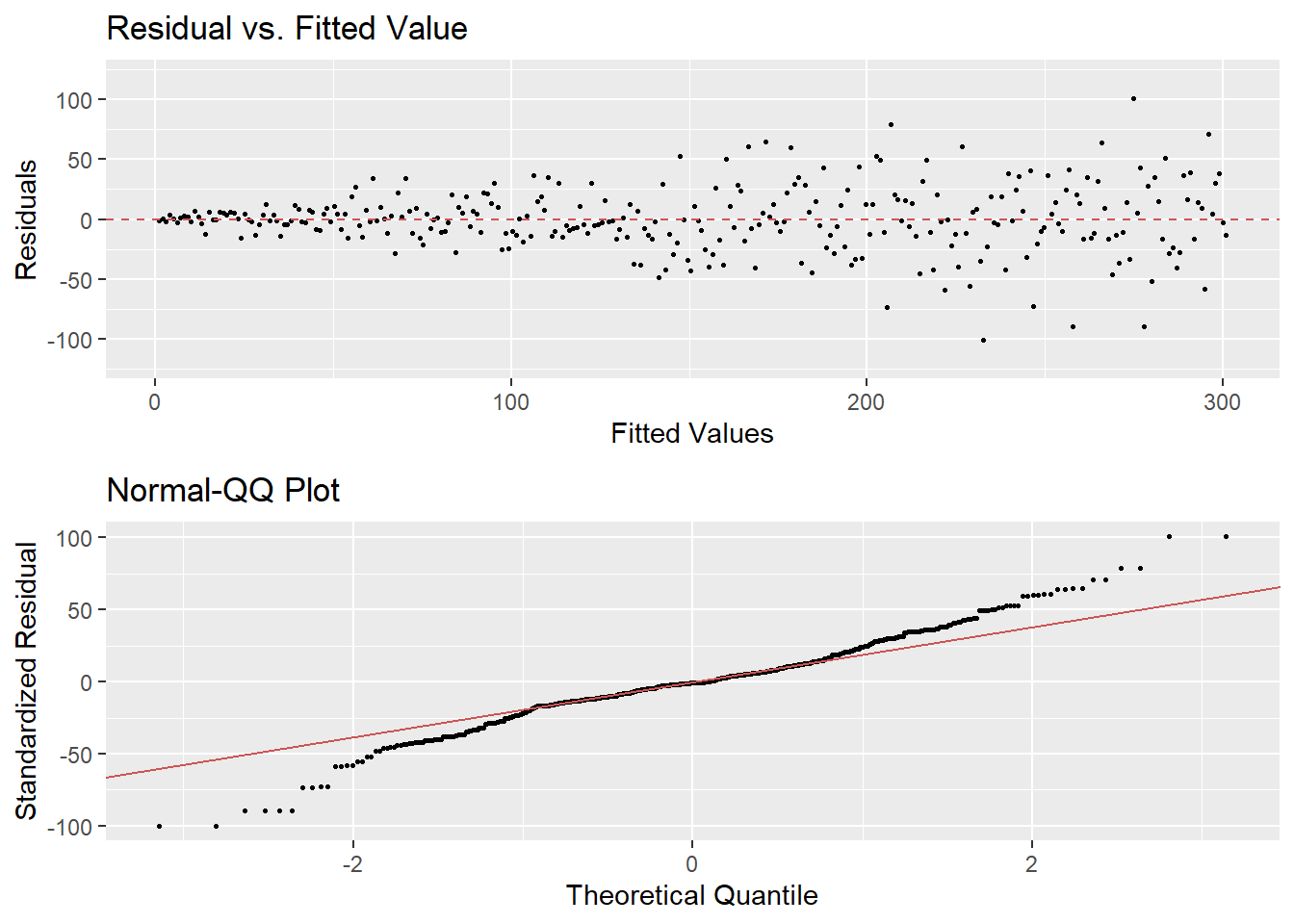
En student ønsker å undersøke sammenhengen mellom pris og størrelsen på leiligheter (m^2). Han bestemmer seg for å samle inn data på solgte leiligheter ukentlig over et helt år. Hva kan være problematisk for en slik strategi?
Anta \(Y_i\) er forandring i BNP fra kvartal \(i-1\) til kvartal \(i\), mens \(x_i\) er forandringen i arbeidsledighet fra kvartal \(i\) til kvartal \(i-1\). Du tilpasser så regresjonsmodellen \[\begin{equation} Y_i = \beta_0 + \beta_1 x_i + \epsilon_i \end{equation}\] Forklar hva forskjellen på et prediksjonsintervall og konfidensintervall er i denne sammenhengen dersom \(x=0\), og hvorfor begge typer intervall er interessante.
Eksamen Vår 2019, Oppgave 2d) og e).