Seminar 1 - Grunnleggende statistikk
- (V20, OPPG 1) Grafen ble publisert av klima- og miljøminister Ola Elvestuen fra Venstre på Twitter 1. november 2019 (men senere tatt bort), og viser norske CO\(_2\)-utslipp (i 1000 tonn CO\(_2\)-ekvivalenter) som funksjon av tid. Venstre gikk inn i regjering sammen med Høyre og Fremskrittspartiet i januar 2018. Denne figuren ble kritisert for å være misvisende. På hvilken måte er den det, og hvordan ville du forandret den for at den skulle være mindre misvisende?
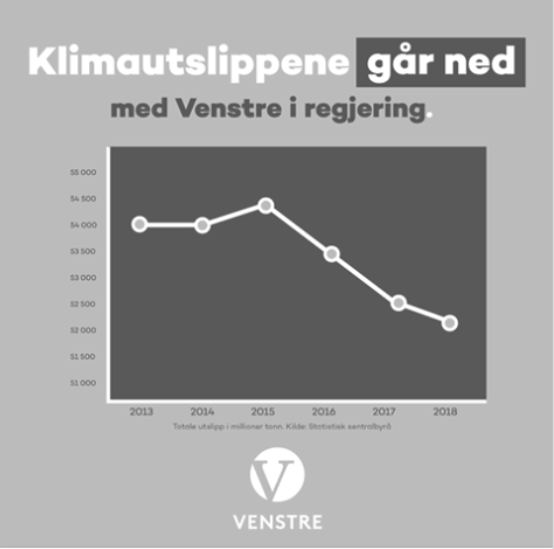
- (V20, OPPG 1) Figuren under ble publisert av Høyre på Facebook 1. november 2019, og viser norske CO\(_2\)-utslipp (i 1000 tonn CO\(_2\)-ekvivalenter) som funksjon av tid. Denne figuren ble også kritisert for å være misvisende. På hvilken måte er den det, og hvordan ville du forandret den for at den skulle blitt mindre misvisende?
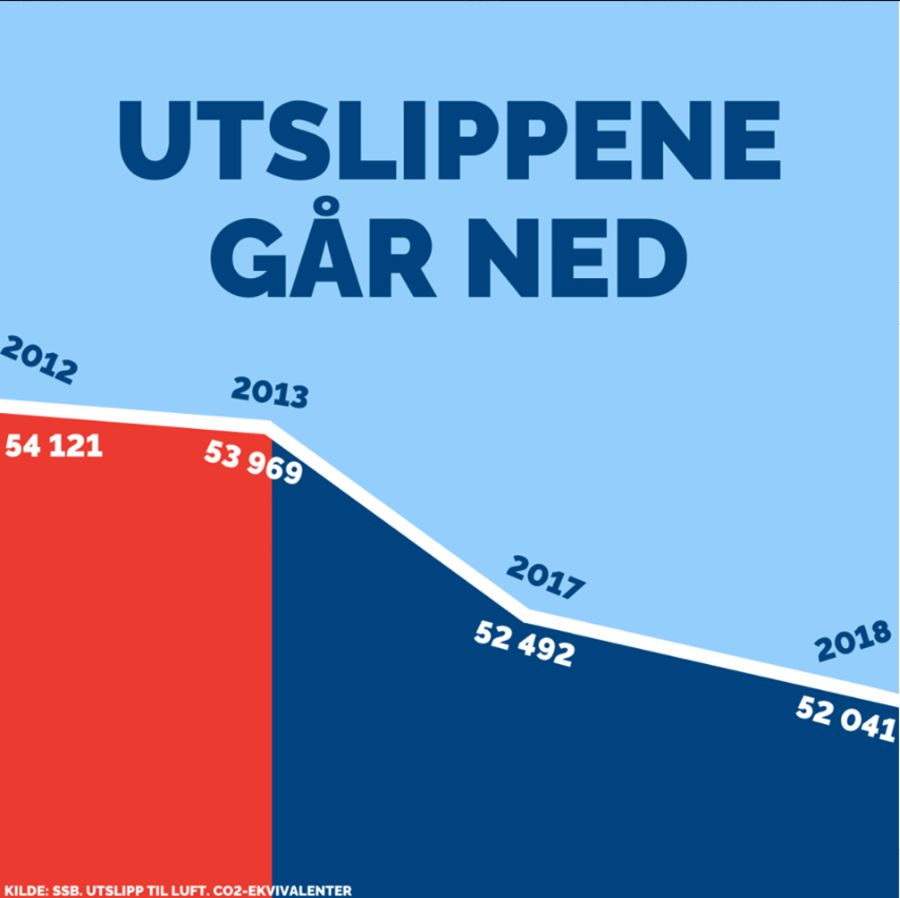
- (V19, OPPG 3) I figuren under ser vi en graf over den norske styringsrenten siden 2013 og anslag over hvilken bane renten skal følge de neste tre årene med fire usikkerhetsintervaller. Bruk figuren til å anslå sannsynligheten for negativ styringsrente ved utgangen av 2022.
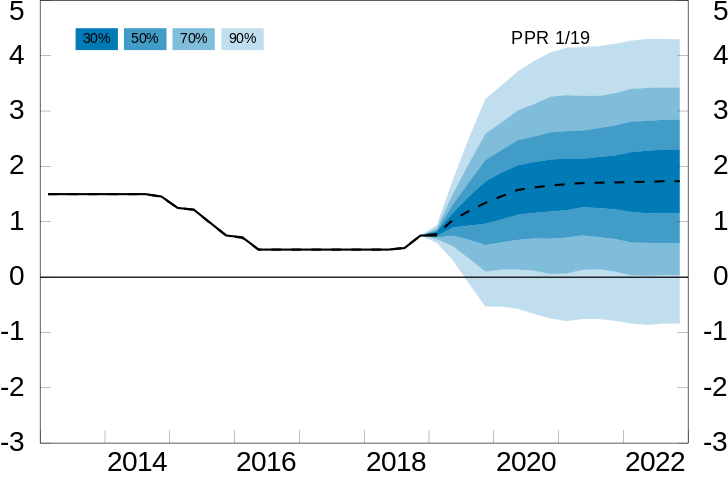
- Florida innførte i 2005 en såkalt “Stand Your Ground”-lov, som i større grad tillater folk å bruke dødelig makt i selvforsvar. Grafen under, som viser utviklingen av dødsoffer i skyteepisoder i Florida, illustrerte mange nyhetsreportasjer etter et drap i 2012, men fikk skarp kritikk i ettertid. Hvorfor det tror du?
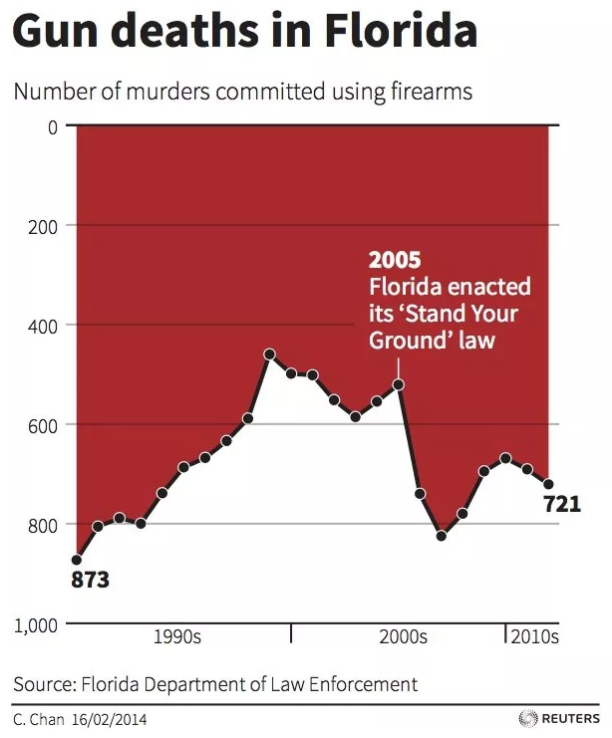
- La oss anta at 50 avgangsstudenter som gikk ut av NHHs masterprogram i fjor svarte på et spørreskjema hvor mye de har i startlønn i sin første jobb. Gjennomsnittslønnen var 450.000, med et standardavvik på 120.000. Anta videre at lønnsfordelingen for årets studenter er den samme (og se bort fra inflasjon).
- Estimer sannsynligheten for at gjennomsnittlig startlønn for 50 responenter i år vil være større enn 450.000.
- Estimer sannsynligheten for at gjennomsnittlig startlønn for 50 responenter i år vil være større enn 500.000.
- La \(X\) være en stokastisk variabel med forventningsverdi lik 5 og varians lik 2. Definer to nye stokastiske variabler \(Y = 2X-1\) og \(Z = X^2 + Y\). Regn ut:
- E\((Y)\) og Var\((Y)\).
- E\((Z)\) og Var\((Z)\).
- La \(X\) være en standard normalfordelt variabel. Du får oppgitt at det medfører at E\((X^3) = 0\). La \(Y = X^2\).
- Vis at korrelasjonen mellom \(X\) og \(Y\) er lik null.
- Er \(X\) og \(Y\) uavhengige?

